

我正在为以下问题寻找快速解决方案:
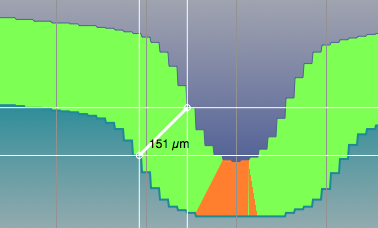
我有一个固定点(比如说白色测量线上的右上角),需要在由等距点组成的曲线(下曲线)上找到最近的点。此外,我对上曲线上的每个点都这样做,以绘制不同颜色曲线之间的距离(三个级别:低于最小值[红色],最小值和最大值之间[橙色]和高于最大值[绿色])。
我目前的解决方案是权衡:我取定点,遍历任意间隔(例如,定点左右各50个单位),计算每对的距离。这节省了一些CPU,但既不优雅也不准确,因为我可能会错过我选择的间隔之外的最小距离。
有更快算法的建议吗?
编辑:等间距意味着所有点在x轴上的距离相同,这对于两条曲线都是如此。我也不需要在点之间插值,这太耗时了。
而不是任意的距离,你也许可以迭代直到“超出范围”。
在你的例子中,假设你从线右上角的上曲线上的点开始。然后垂直向下下降,你得到大约200微米的距离(按我的眼睛)。
现在你可以从这里移动测试点,直到水平距离为200um。除此之外,不可能得到小于200um的距离。
向左移动,距离下降,直到你找到150微米的最小值,然后又开始上升。一旦你在上一点的左边150微米,再次,不可能超过你找到的最小值。
如果你先向左走,你就不必向右走这么远,所以作为一个优化,要么沿着距离下降的方向走,要么从中间同时向两个方向走。
我不知道um 50单位是多少,所以这可能比你现有的要慢或快。不过,它确实避免了错过较低值的风险。
因为你要对下曲线上的同一组点进行大量测试,所以你可以通过忽略这些点形成一条曲线的事实来改进这一点。把它们都粘在k-d树或类似的树上,然后重复搜索。这叫做最近邻搜索。
将此问题识别为最近邻搜索问题可能会有所帮助。该链接包括关于用于此目的的各种算法的良好讨论。如果您可以使用C而不是直接使用C,ANN看起来是一个很好的库。
看起来这个问题以前也被问过。
我们可以标记顶部曲线y=t(x)和底部曲线y=b(x)。标记最接近函数x_b=c(x_t)。我们知道最接近函数是弱单调非递减的,因为两条最短路径永远不会交叉。
如果你知道距离函数d(x_t,x_b)对于每个固定的x_t只有一个局部最小值(如果曲线足够平滑就会发生这种情况),那么你可以通过“行走”曲线来节省时间:
- start with x_t=0, x_b=0
- while x_t <= x_max
-- find the closest x_b by local search
(increment x_b while the distance is decreasing)
-- add {x_t, x_b} to the result set
-- increment x_t
如果你期望x_b足够平滑,但你不能假设,你想要一个确切的结果,
在两个方向上走曲线。在结果一致的地方,它们是正确的。在它们不一致的地方,在两个结果(最左边和最右边的局部最大值)之间运行完整的搜索。以这样的顺序(二元除法)对“模糊块”进行采样,以允许由于单调性而进行最多的修剪。
作为中景:
沿两个方向走这条曲线。如果结果不一致,请在两者中进行选择。如果你能保证每个固定x_t最多有两个局部极大值,这就产生了最优解。仍然有一些病理情况没有找到最优解,并且包含一个局部极小值,其两侧还有两个比这个更差的局部极小值。我敢说,找到一个解远不是最优的情况是不常见的(假设光滑y=b(x))。